最近研究盘长结理论发现的新型盘长结

hubo5563 于 2021-3-6 08:40 编辑 盘长结是古老的中国结，是咱们老祖宗遗留下来的基本结之一。它是由基本单元四耳酢浆草单元扩展而成，四耳酢浆草单元属于正方形，它在平面上是无限可扩展的，所以后来就发展变化出多种形状。基于这个原理，我研究了正多边形在平面扩展与盘长单元的属性，找到一批新型盘长结。 正三角形对应的三耳酢浆草结，它可平面无限扩展，由它扩展的盘长就是减线盘长，这类盘长由陈夏生老师发现，并发表在中国结3书上。 正方形对应的是四耳酢浆草结，它的平面扩展就是普通的盘长。 正六边形也可平面无限扩展，它对应的是六耳团锦共用套，由谭蓬竹老师研究发现。 除此之外，再无单一的正多边形可以在平面上无限扩展。然而可以用多个正多边形混合平铺平面。利用这些是否能设计出新型盘长，实际上是可以的。 第一种，4边形与3边形能平铺平面，对应的就是4-3盘长：由于这种结构不是太好看，没有为其添加耳翼：

43仿真.JPG (1023 KB, : 0)

2021-3-2 15:03

上面那个4-3盘长由于中间有单元不正规，使得它不是一个完备盘长，就是说有的形状是编不成的。这个盘长只是证明它的存在，不建议学习它。如果你想研究它的不完备性，可以深入研究，寻找规律。 下面是4-3盘长的正式形状，这个盘长是完备的，任何形状都能编成功的。不过盘长的花纹不是好看的，编法也没有成熟的方法，暂时也不要学这个。

05-43盘长.JPG (748.28 KB, : 0)

2021-3-6 08:31

第二种正六边形和正三角形可平铺平面，对应的是6-3盘长，如下：

6-3六边形盘长01.jpg (837.47 KB, : 0)

2021-3-2 15:02

这样的盘长是完备的，用它可以设计任何形状。 第三种是正8边形与正方形混合可铺满平面，由于单元可以有多种设计，共找到三种新型盘长： 1、8-4盘长，它是有穿3包3的8耳团锦单元与酢浆草单元按正八边形与正方形平铺平面的规则排列的。

8-4盘长01.jpg (680.13 KB, : 0)

2021-3-2 15:02

2 、八角孔盘长，它的扩展单元是不完整的，因此，用单元随便排列，有的情况是无法实现盘长的，需要专门设计形状。

8角孔盘长01.jpg (535.62 KB, : 0)

2021-3-2 15:02

3、金钱盘长，由于花纹隐含古代的铜钱花纹，所以命名金钱盘长：

金钱盘长.jpg (830.87 KB, : 0)

2021-3-2 15:03

金钱盘长2.jpg (1019.94 KB, : 0)

2021-3-2 15:03

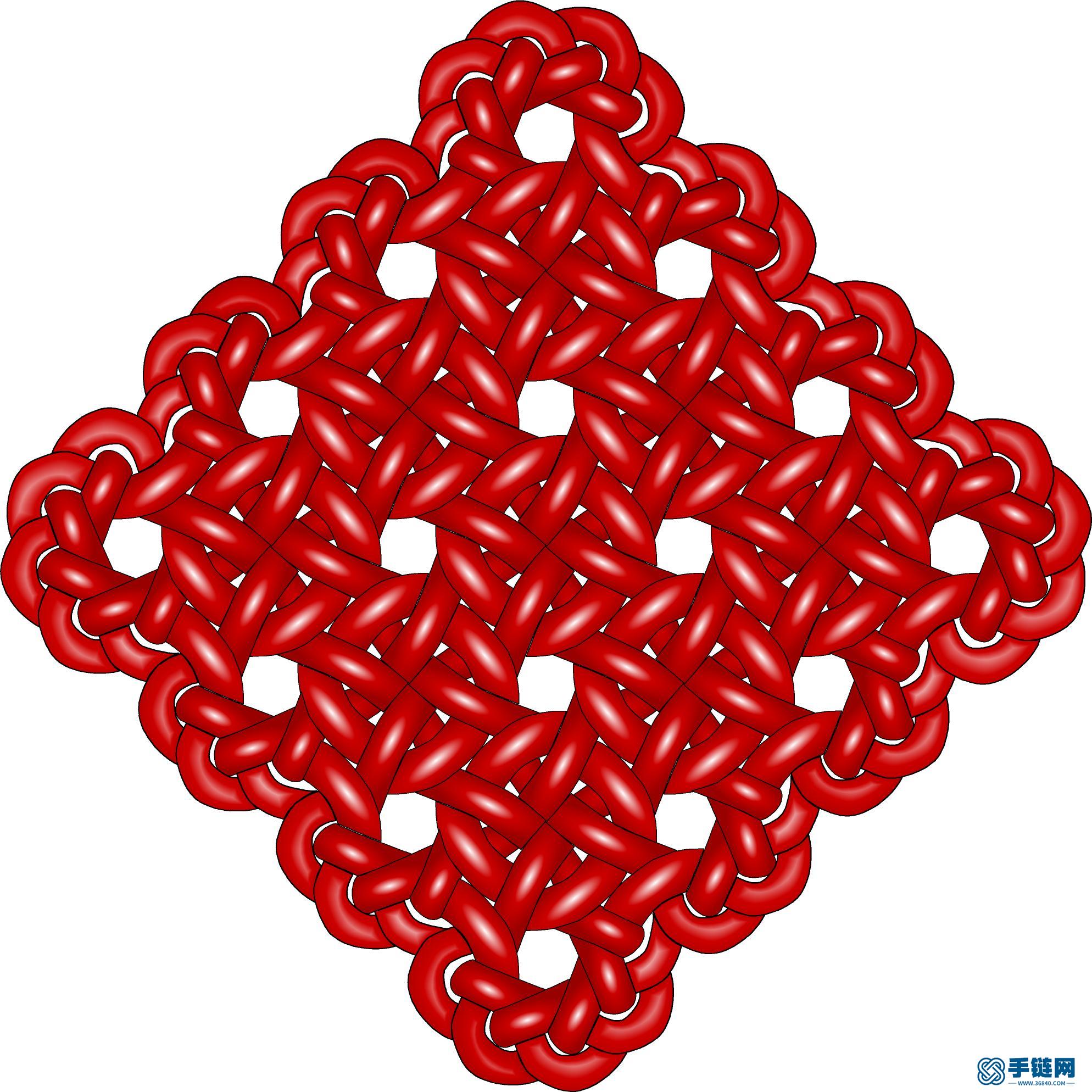
金钱盘长4乘401.jpg (373.71 KB, : 0)

2021-3-2 15:03

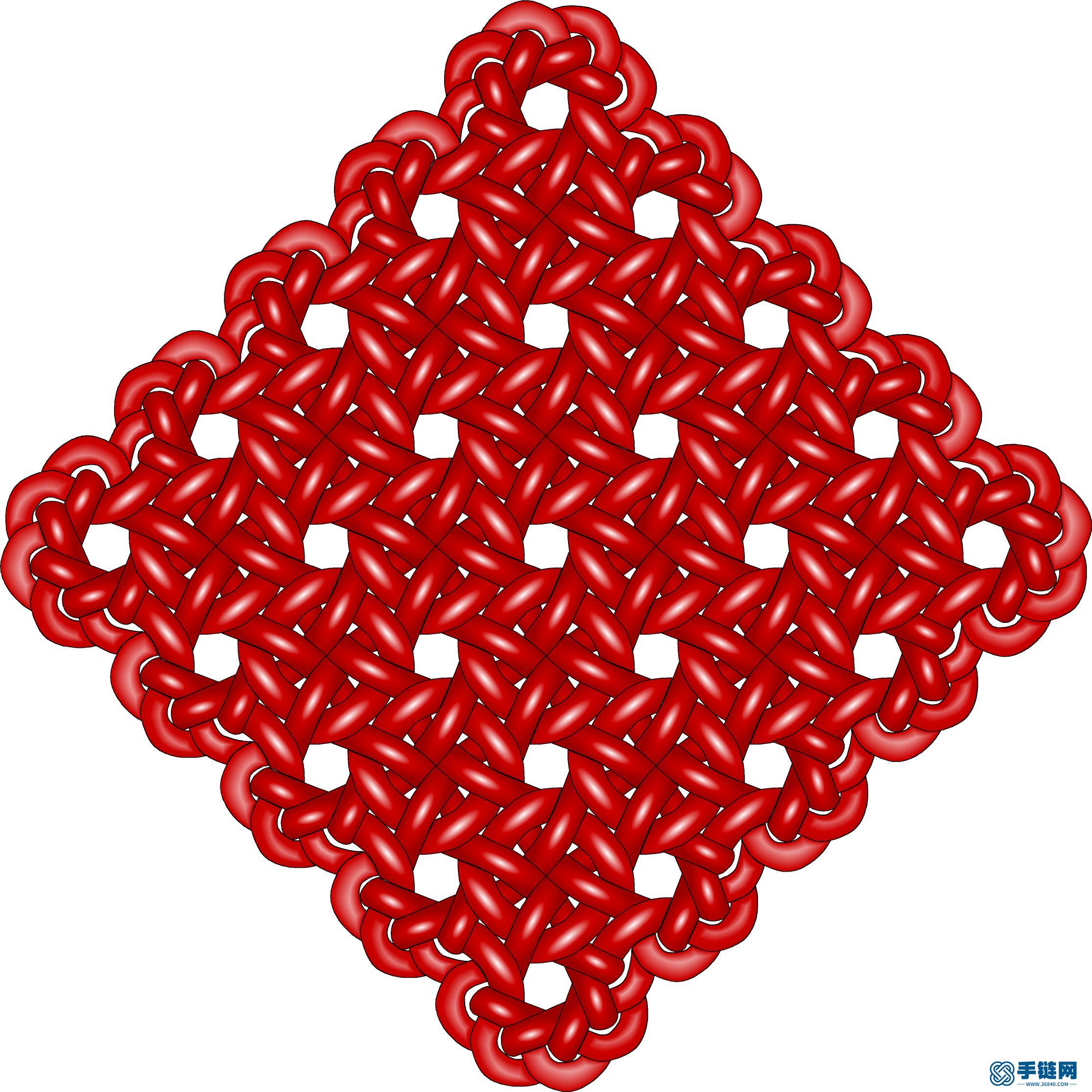
金钱盘长5乘5-01.jpg (484.33 KB, : 0)

2021-3-2 15:03

金钱盘长6乘6.jpg (533.66 KB, : 0)

2021-3-2 15:03

第四种是正十二边形与正三角形可平铺平面，对应的盘长12-3，它的扩展单元是十二耳穿4包4的团锦与三耳酢浆草单元：

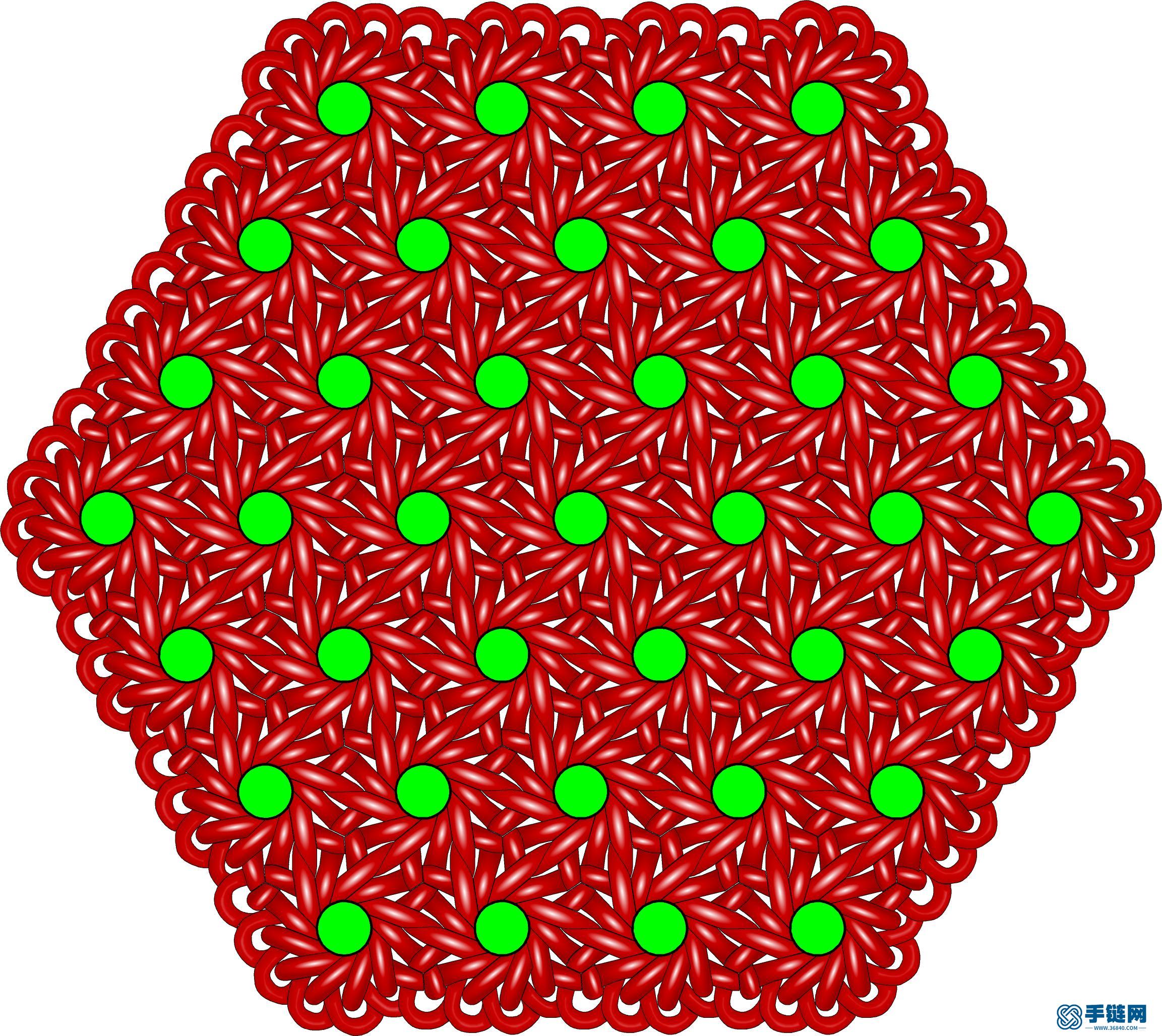
12-3六边形边长4单元.jpg (774.81 KB, : 0)

2021-3-2 15:02

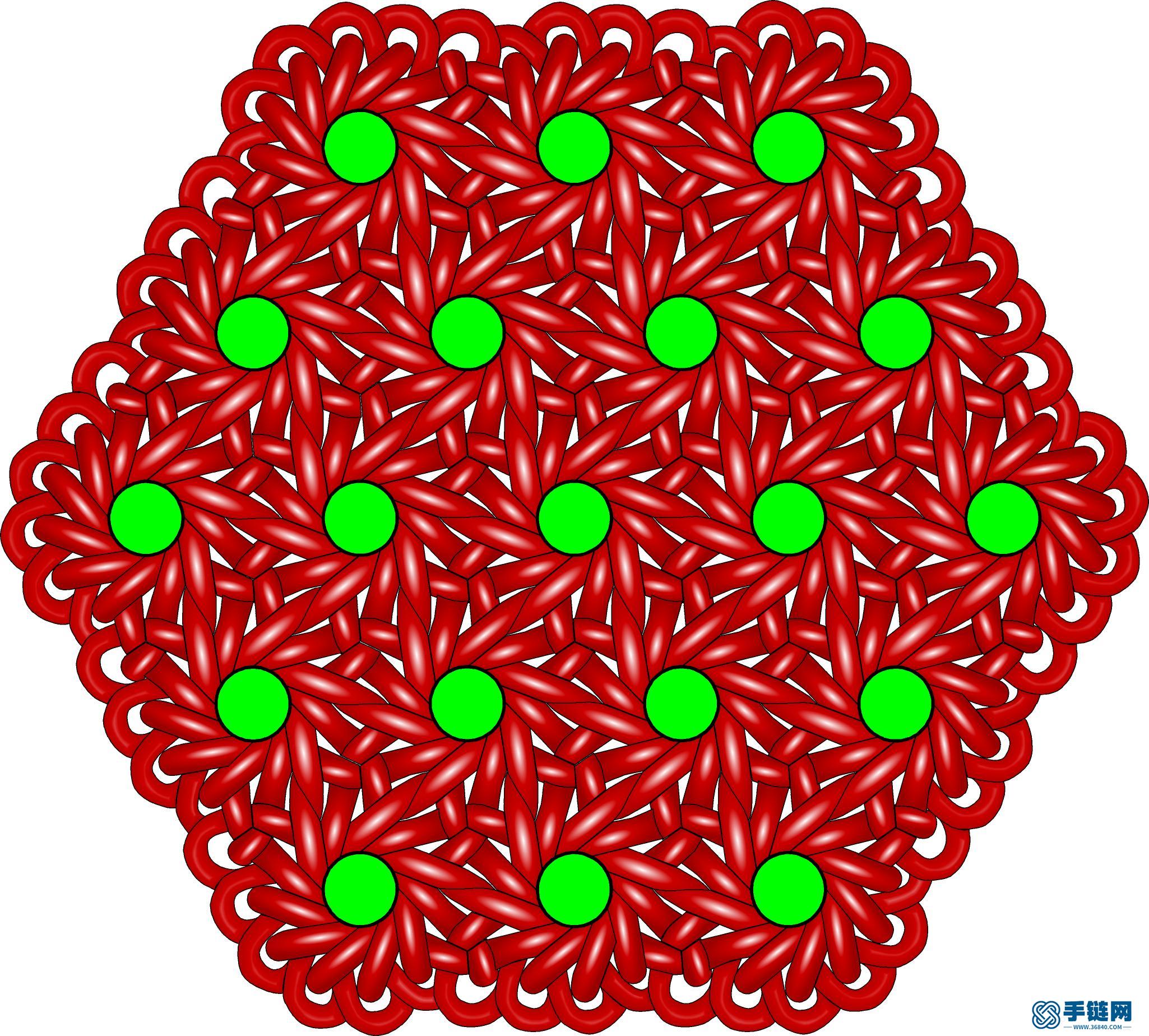
12-3六边形边长3单元.jpg (556.46 KB, : 0)

2021-3-2 15:02

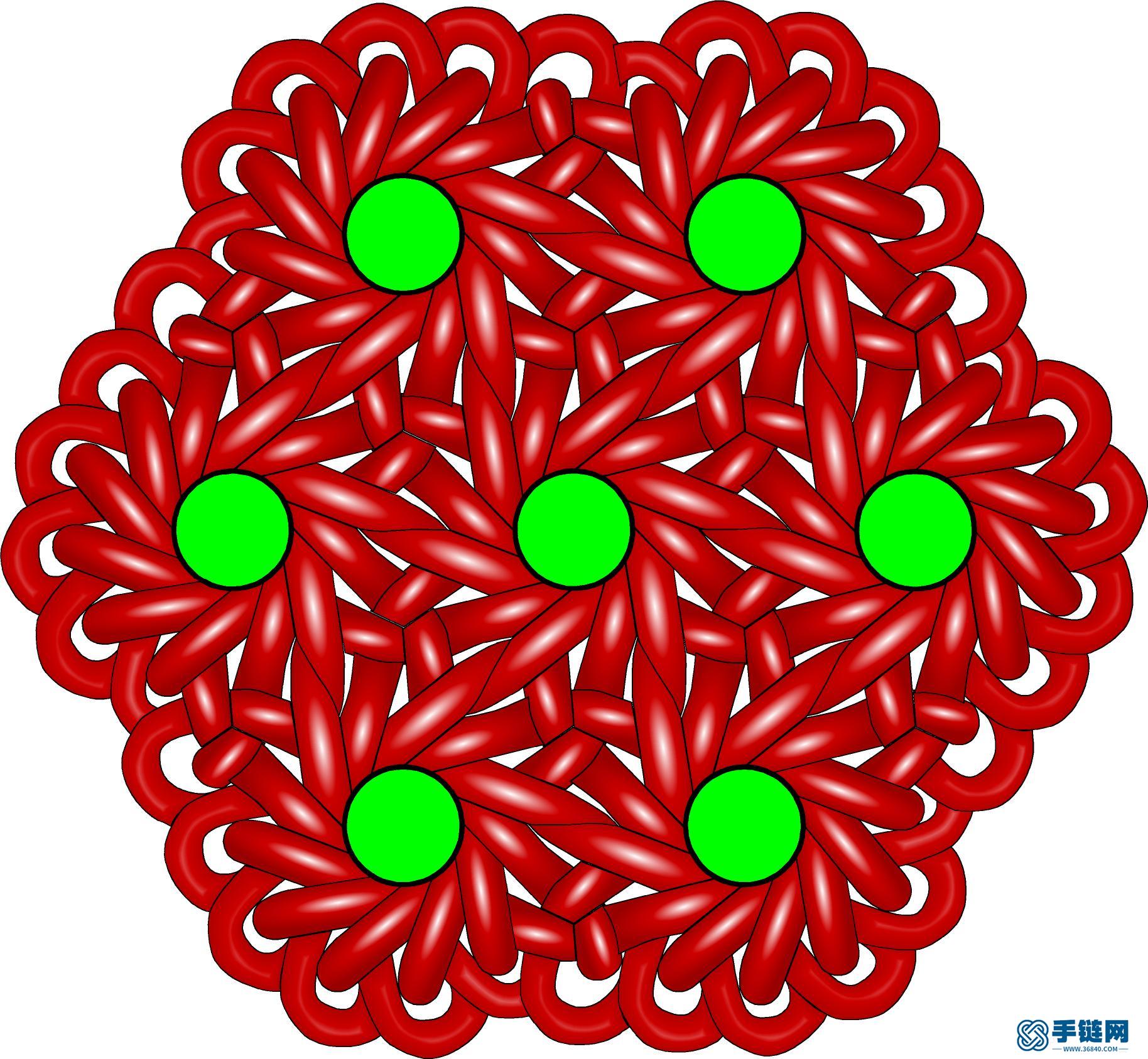
12-3六边形边长2单元.jpg (365.45 KB, : 0)

2021-3-2 15:02

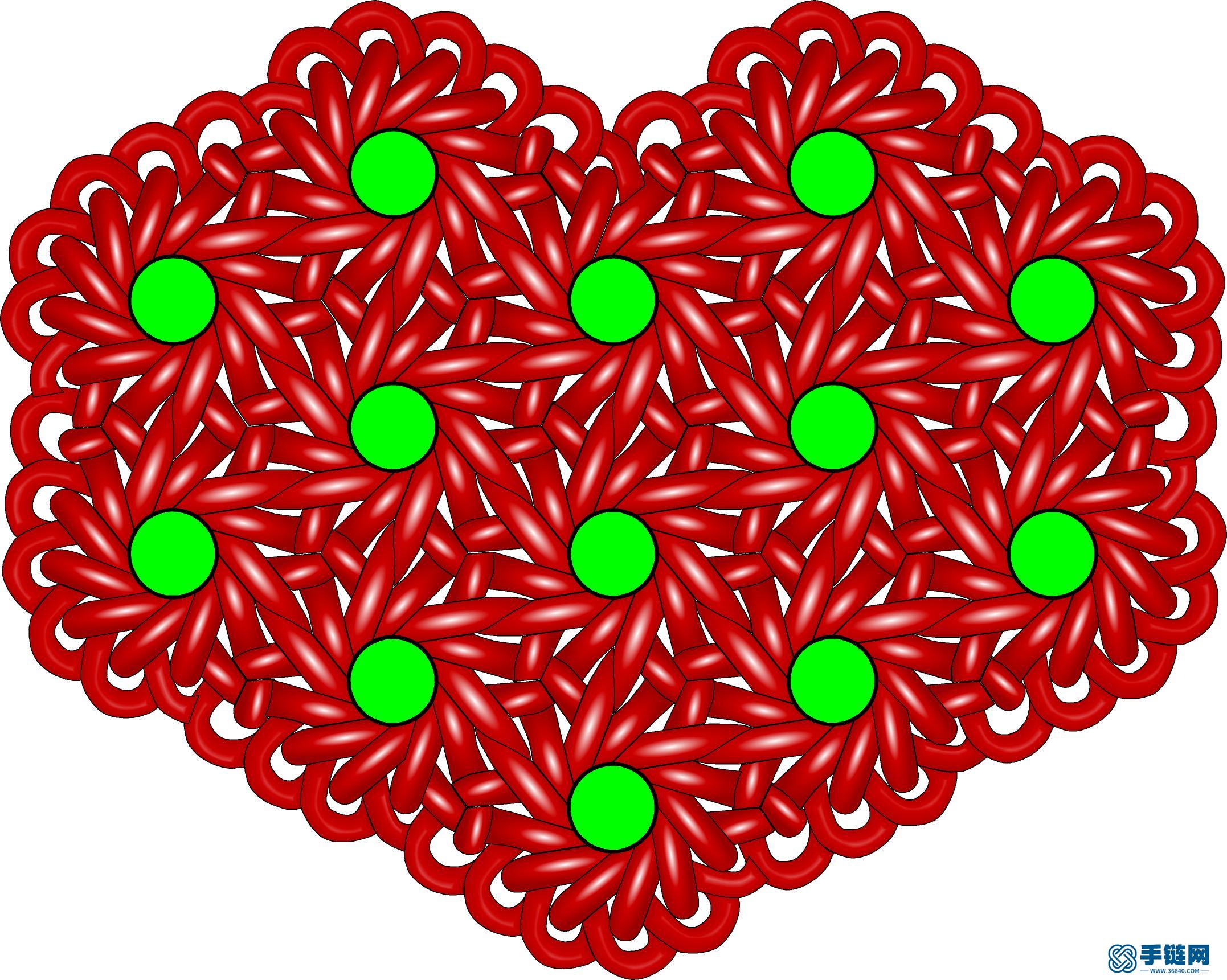
12-3心形01.jpg (489.4 KB, : 0)

2021-3-2 15:02

这个结也是完美的，可以设计任何形状。 除此之外，可以有三种多边形混合铺满整个平面，也可设计盘长。 第一种正六边形、正方形、正三角形混合可铺满平面，利用这个规律，设计出来的6-4-3盘长：

643盘长01.jpg (630.68 KB, : 0)

2021-3-2 15:03

第二种正十二边形、正方形、正三角形可平铺平面，如果用12耳团锦单元，4耳酢浆草单元加三耳酢浆草单元设计，就会形成圈，因此，我设计了两种没有圈的盘长，第一种去掉四耳酢浆草，形成12-3-空4盘长，由于没有真正的12-4-3盘长，就命名其12-3-4盘长吧：

12-4-3正方形8单元.jpg (1.13 MB, : 0)

2021-3-2 15:02

12-4-3正方形4单元.jpg (566.11 KB, : 0)

2021-3-2 15:02

12-4-3正方形5单元.jpg (681.35 KB, : 0)

2021-3-2 15:02

12-4-3磬结6乘3单元.jpg (545.73 KB, : 0)

2021-3-2 15:02

第二种是合并四个正三角形与正方形，它是一个尖角菱形，接近正方形，由于绳结不是刚性的，它可柔性变化，所以在这个位置放入一个2乘2酢浆草单元，就形成如下结：

12-4盘长4乘4.jpg (676.89 KB, : 0)

2021-3-2 15:02

12-4盘长3乘3.jpg (533.16 KB, : 0)

2021-3-2 15:02

12-4盘长5乘5.jpg (754.5 KB, : 0)

2021-3-2 15:02

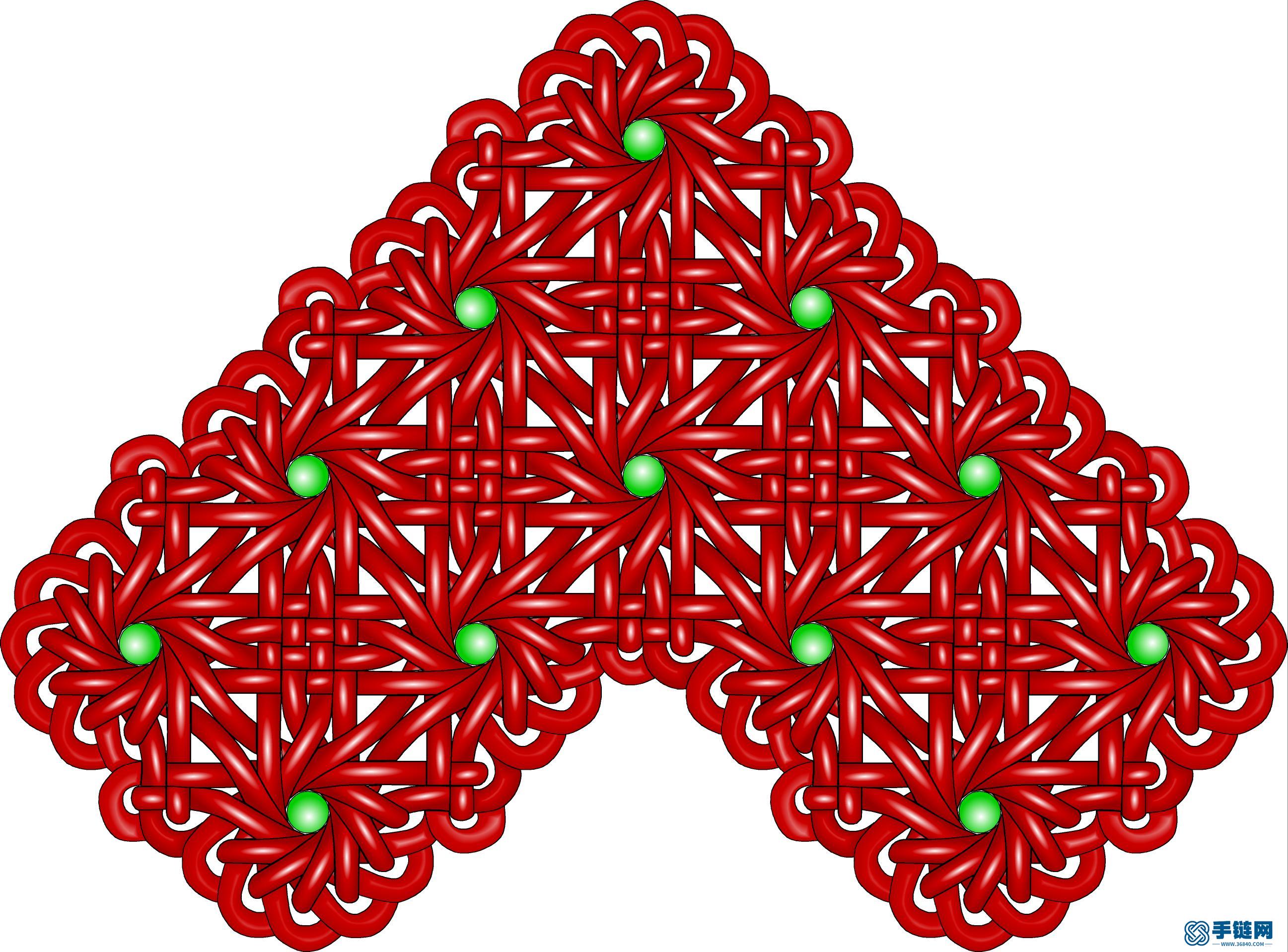
12-4磬结4乘2.jpg (576.42 KB, : 0)

2021-3-2 15:02

就叫它12-4盘长吧，它是一个完备盘长，用它可以设计任何形状。第三种 是正十二边形、正六边形、正方形可平铺平面，对应的盘长就是12-6-4盘长。

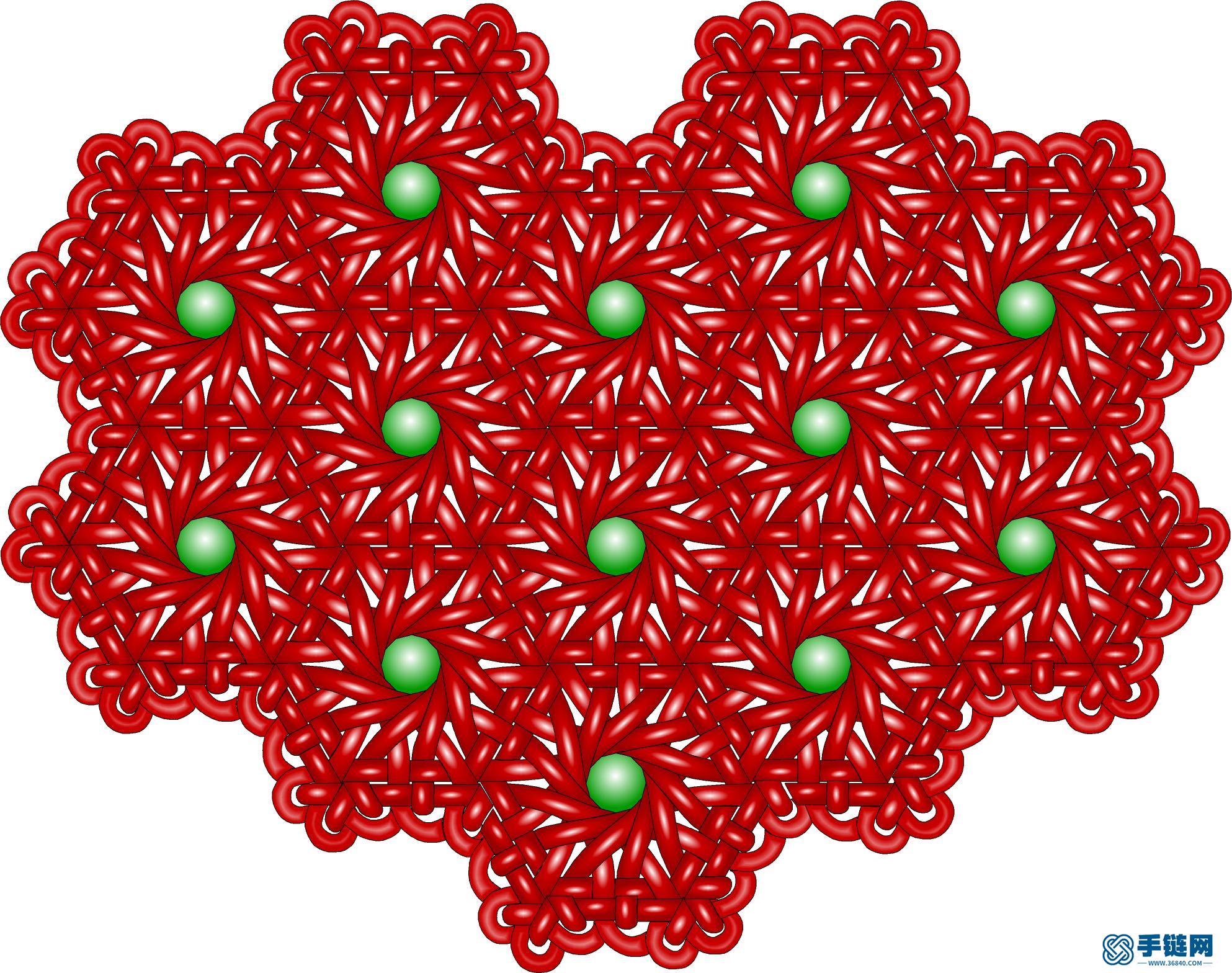
心形.jpg (526.49 KB, : 0)

2021-3-2 15:03

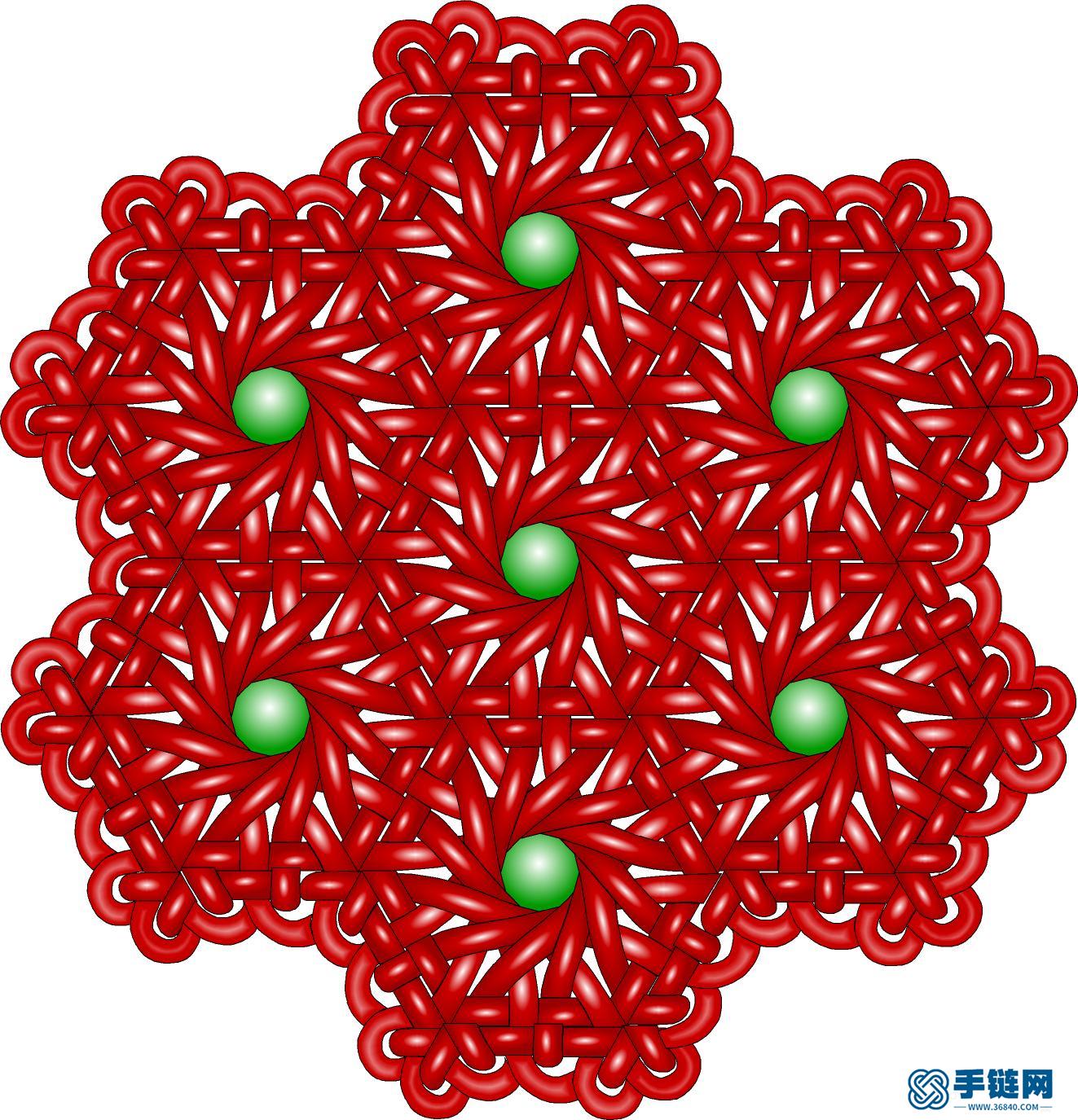
六边形.jpg (312.12 KB, : 0)

2021-3-2 15:03

这个也是完备盘长，可以设计任意形状。 另外，基于正六边形平铺平面的原理，设计不同结构的单元，还找到了12角孔盘长：

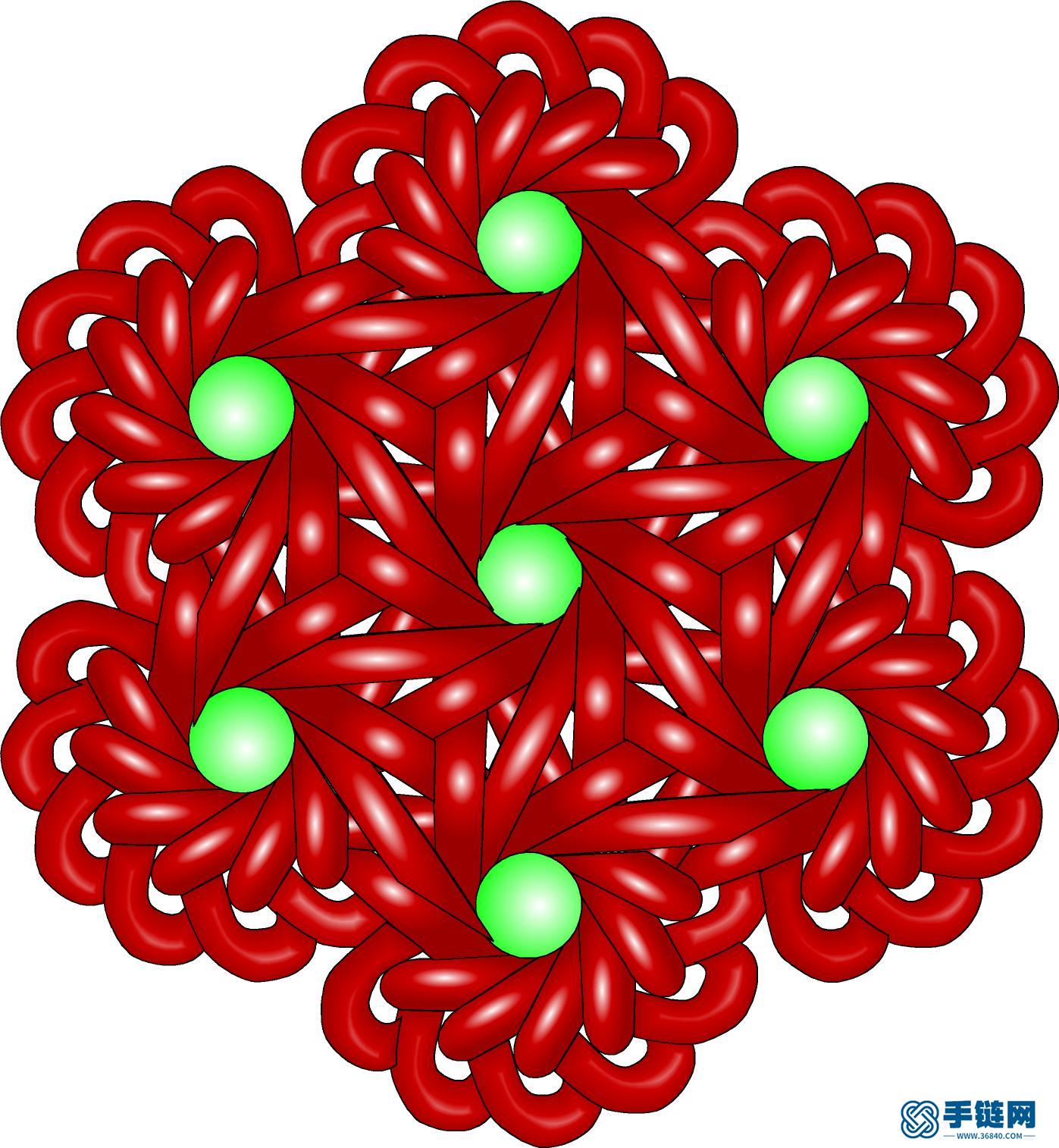
12角孔纹盘长.jpg (238.87 KB, : 0)

2021-3-2 15:02

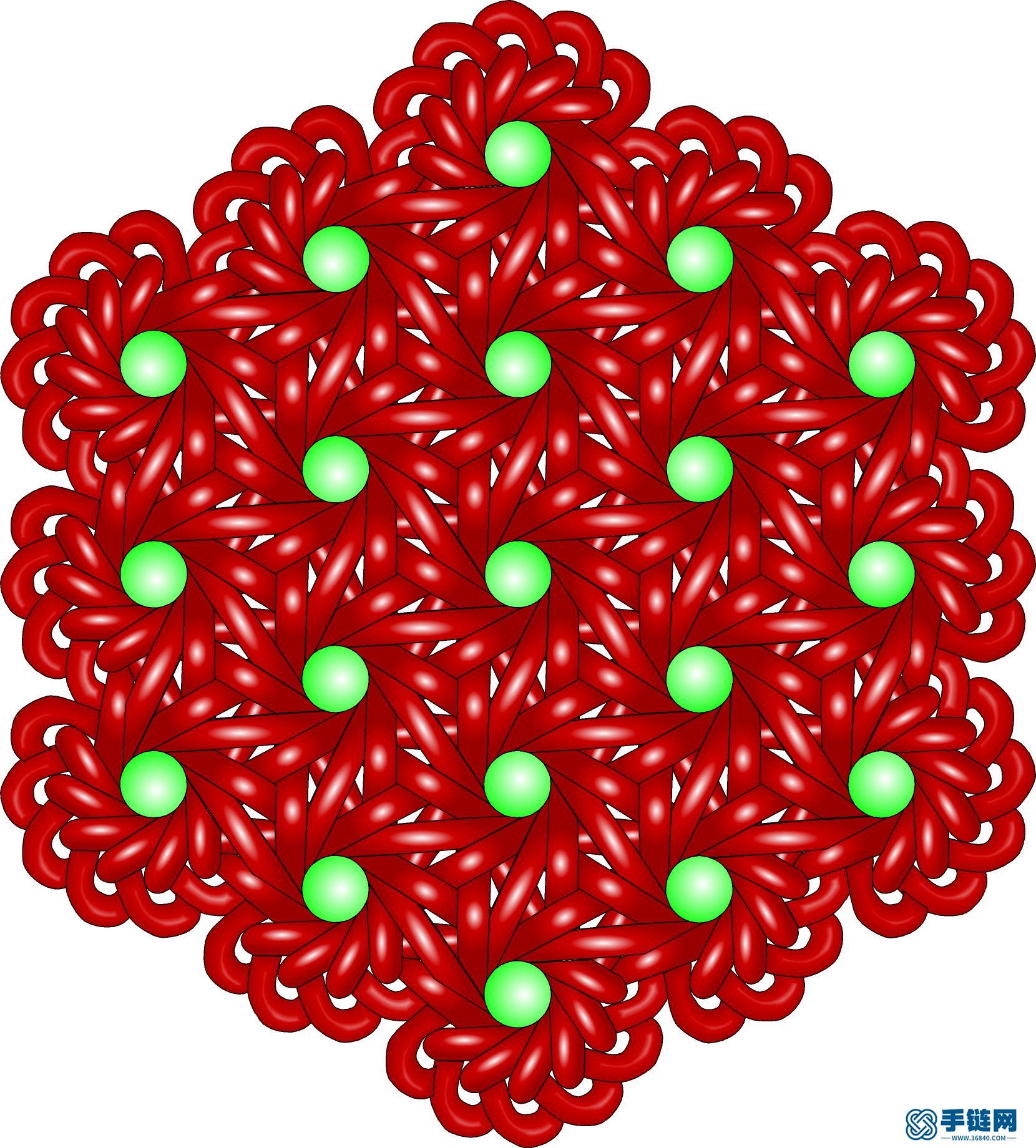
12-3-六边形.jpg (396.03 KB, : 0)

2021-3-2 15:02

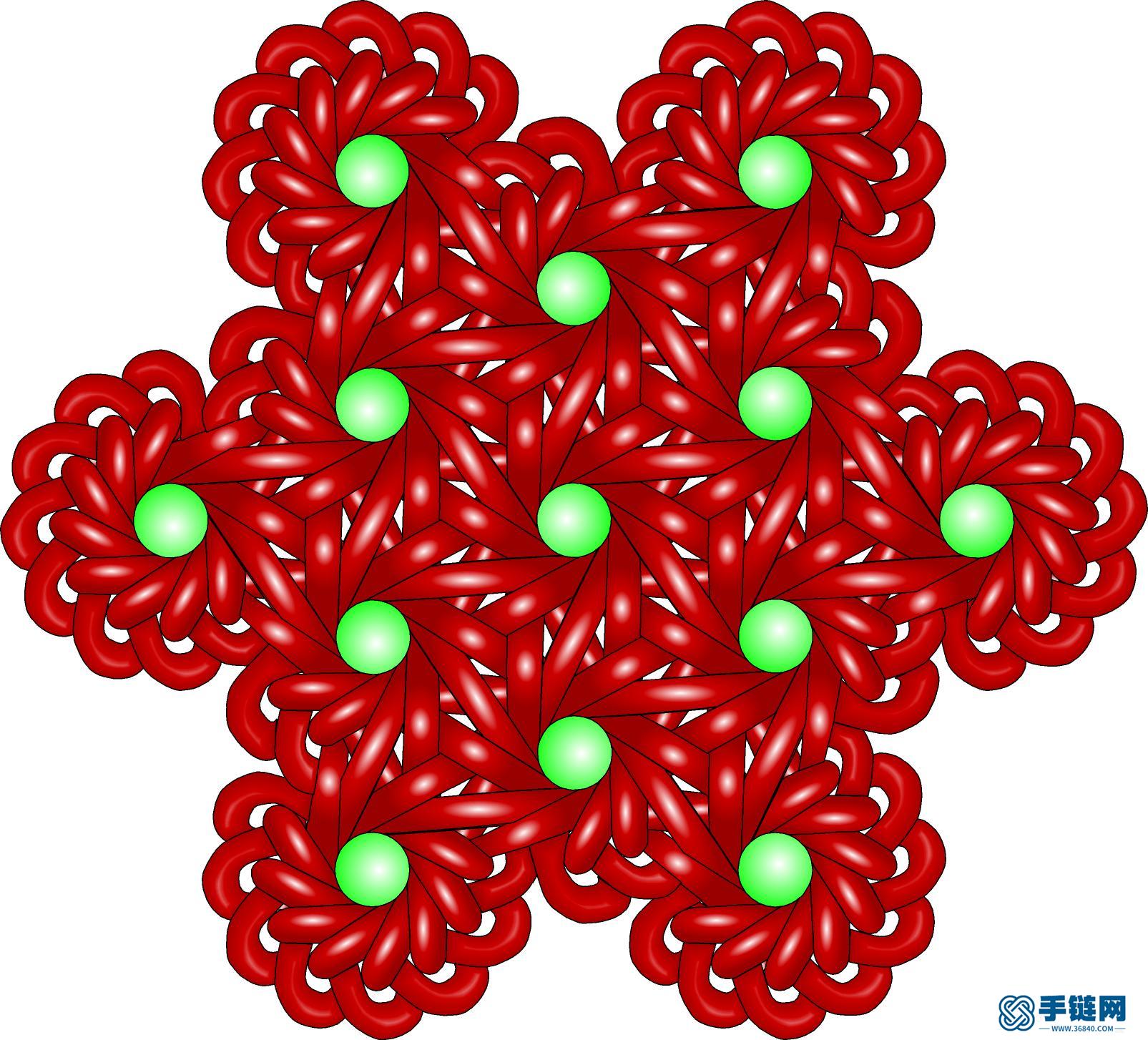
12-1-六角形.jpg (289.32 KB, : 0)

2021-3-2 15:02

以及它的姊妹盘长，命名雪花纹12角孔盘长：

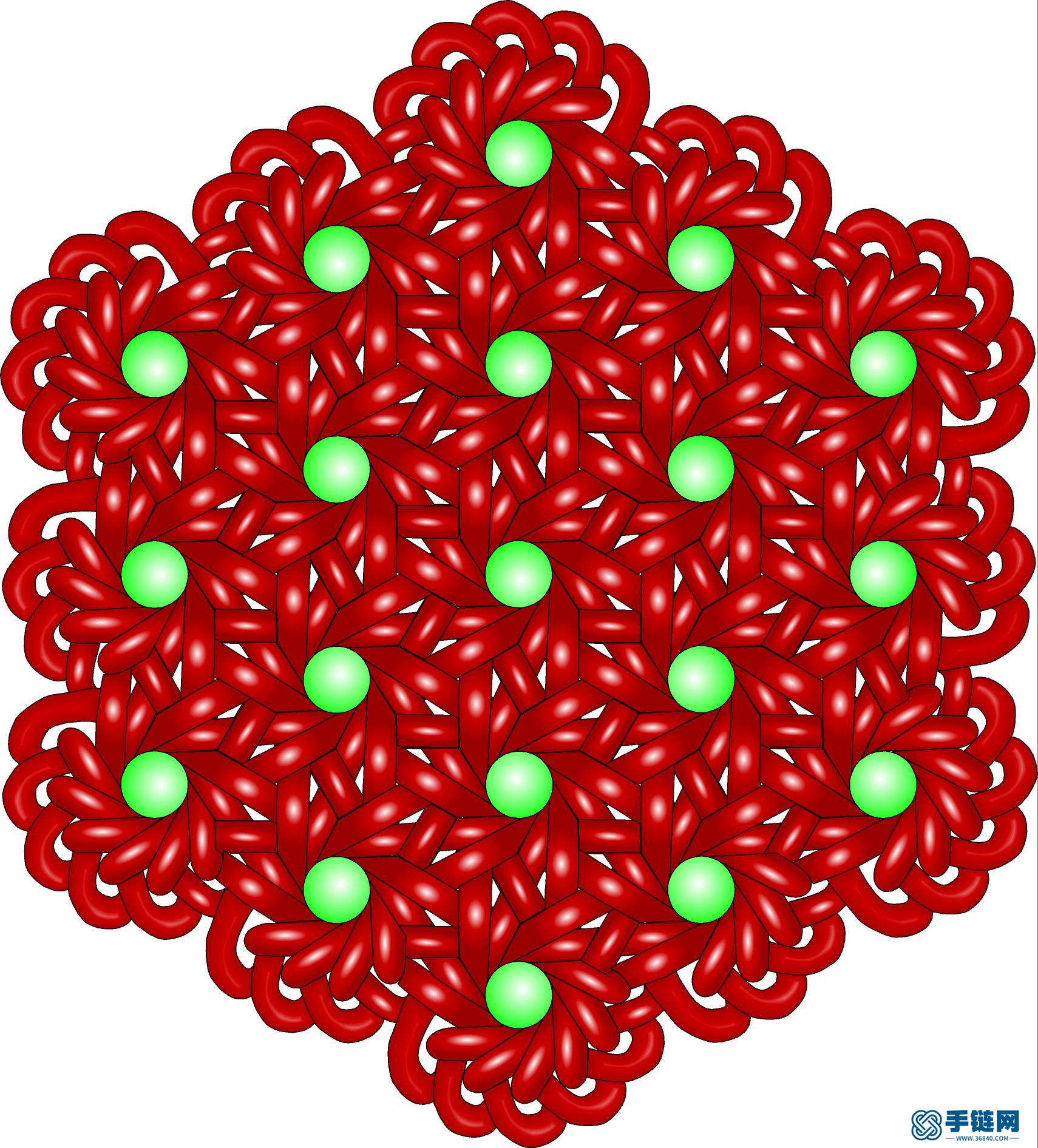
12-1-3六边形.jpg (417.69 KB, : 0)

2021-3-2 15:02

12角孔雪花纹盘长.gif (453.23 KB, : 0)

2021-3-2 15:03

这两种盘长不是完备的，就是只有特定形状才能编成盘长。在研究它的编法时，无意发现了六瓣花盘长：

6-3-六边形.jpg (430.08 KB, : 0)

2021-3-2 15:02

六瓣花盘长小六边形17.jpg (345.71 KB, : 0)

2021-3-2 15:03

六瓣花盘长小六边形18.jpg (297.29 KB, : 0)

2021-3-2 15:03

星形01.jpg (134.7 KB, : 0)

2021-3-2 15:03

这种盘长也不是完备的，只有特定形状才能编成盘长的。这个纹路和竹编的龟甲纹编一样，应该叫做龟甲纹盘长。 研究它的编法时，又发现了一种斜纹不对称盘长：

斜纹盘长01.jpg (425.24 KB, : 0)

2021-3-2 15:03

这个不是酢浆草单元的扩展，编起来难一些。 就介绍到这里吧。.本文来源于中国结中国结论坛

https://www.zhongguojie.org/